0 引言
在2021年全球领导人气候峰会上，我国提出将力争2030年前实现“碳达峰”，2060年前实现“碳中和”，这是为推动共同构建人与自然生命共同体所做的大国担当。“双碳”目标是一项系统工程，电力行业将担负主力军作用。除了众所周知的CO2减排之外，电网系统中SF6气体减排亦引起了人们的广泛关注。SF6的绝缘强度高(约为空气的3倍)、液化温度低(–64 ℃)、灭弧能力强且具有自恢复特性。自19世纪70年代起，SF6气体就被用作各种高压电气设备的绝缘介质，包括气体绝缘开关(GIS)、断路器(GCB)、输电管道(GIL)等。遗憾的是，SF6是已知的最强温室气体，其全球变暖潜势(global warming potential, GWP)高达24 300，即1吨SF6相当于24 300吨CO2排放。虽然目前SF6的大气浓度只有CO2的0.2%左右，但SF6难以降解，极易在大气中积累。因降解机理差异，SF6的大气寿命仍存争议[1]，从最初的3200年到(1937±432)年、1120~1475年、580~1400年不断变更，但GWP降低仅5%左右。根据实验观测，大气中SF6体积分数已从1995年的3×10–6达到2020年的10×10–6，年增长率也从0.22×10–6提高了50%。IPCC预计2100年大气中SF6体积分数将达到65×10–6，导致全球温升约0.03 ℃。因此，采用环境友好型绝缘气体替代SF6，对抑制全球变暖具有重要意义。
自2012年起我国陆续发布了针对SF6气体的相关标准，包括使用和回收管制措施。随着我国电气行业的迅猛发展，我国电网装机容量已超过2000 GW，从1980年仅3%世界占比增加到现今30%以上，导致SF6排放迅速增加。仅就中压开关柜而言，因生产、运维、替换、泄漏等因素，我国一年就排放约1800吨SF6，对应CO2排放当量约4200万吨。Simmonds等人综述了全球SF6排放分布特征[2]，发现在1978—2018的40年内，全球SF6年排放量已增长到9000吨，其中我国所占比重迅速增加，远高于西欧国家，且一直占据东亚地区SF6总排放的70%左右，主要分布在华北、四川、长三角、珠三角等地区。鉴于SF6在电气应用上产生的巨大温室效应，SF6减排对我国能否兑现“双碳”承诺至关重要，寻找环保型SF6替代绝缘气体已迫在眉睫。
本文综述了迄今寻找SF6替代气体的相关实验与理论研究进展，特别是围绕绝缘强度、液化温度、温室效应、安全性能(毒性、燃烧)、灭弧特性等关键指标所开展的多维度构效关系、气体虚拟筛选以及分子设计研究，总结了关于各维度理论模型的代表性进展，并分析了相应的优缺点，最终提出了一套切实可行的发现新型环保绝缘气体的技术方案，为加快实现电气设备中SF6的完全替代提供理论依据。
1 寻找SF6替代气体的挑战
事实上，寻找绝缘与开断性能优于SF6的气体一直是电气领域基础研究的热点[3-8]。早在20世纪80年代，西屋研究发展中心联合杜邦公司系统考察了近400种气体，就绝缘强度、开断特性、蒸气压、碳化、扩散、热老化、毒性等方面与SF6进行比较，筛选出约50种气体，但最终发现任何单质气体的性能均无法全面优于SF6。当某些方面性能超越SF6时，必定在另一些方面不及SF6。经过近半个世纪的实验与理论研究，人们陆续提出了一些可能替代SF6的候选绝缘气体，分子结构如图 1所示，相应的绝缘强度、沸点、毒性等参数列于附表 A1。
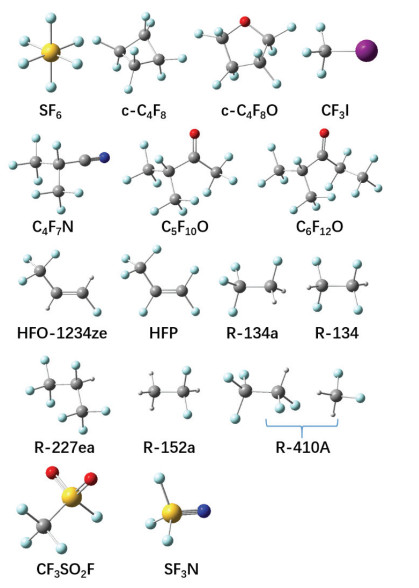图 1 代表性SF6替代气体的分子结构Fig. 1 Molecular geometries of the prototypical replacement gases for SF6
目前在研或已有部分电气应用的替代气体，大多从环保制冷剂(R-134a, R-227ea, R-134, R-152a, R-410A, HFO-1234ze等)和灭火剂(C6)中通过试错试验获得。替代气体的绝缘强度普遍高于或接近SF6，但是所有气体的沸点均远高于SF6，其中某些在室温下甚至呈液态(例如C5、C6)，极大限制了气体的应用范围。另外，在电气设备中普遍采用较高气压(≥0.5 MPa)，即使SF6气体也在−30 ℃时出现液化。因此，通常需采用添加低沸点缓冲气体(例如CO2、N2、CF4、N2O等)的办法以降低液化温度。另一方面，只有含不饱和化学键(例如C=C、C=O、C≡N、S≡N)或含氢原子的分子，GWP才远低于SF6，但同时会导致化学稳定性变差，譬如HFO-1234ze气体放电极易碳化，且在潮湿空气中易燃。较早期研究的c-C4F8的GWP仅为SF6的1/3，环保性能较差；另一种CF3I气体，绝缘强度和液化温度尚可，但其被列为致癌物，且因包含I原子易导致碘沉积，且具有一定破坏臭氧层的可能。
Khan等人对一系列环保制冷剂的绝缘特性开展了系统研究[9]，发现R-134a和R-410A是两种较为优秀的环保绝缘气体，建议可作为SF6替代气体使用。另外，近年来HFO-1234ze也受到较多关注。特别值得一提的是，HFO-1234ze与SF6气体之间存在“正协同”效应[10]：当SF6体积分数超过10%时，HFO-1234ze/SF6混合气体的绝缘强度高于SF6和HFO-1234ze，SSD实验表明可能因HFO-1234ze能够有效降低自由电子能量所致。
目前最为成功的SF6替代气体应为3M公司研发的七氟异丁腈(C4)。虽然有机腈化物的液化温度、GWP、毒性较高，但得益于C4与缓冲气体CO2的良好协同效应，仅需将4%~10%体积的C4与CO2混合，绝缘强度即可与SF6相当，同时毒性和GWP能降低约一个数量级、液化温度可低至−30 ℃。另外，C4的热分解温度虽然较低，仅为650 ℃，但借助于大量CO2缓冲气体，C4/CO2混合气体的稳定性较好，亦能保持一定的灭弧能力。2016年GE和Alstom公司将C4/CO2混合气体(g3)成功用于各种高压电气绝缘设备(GIL、GIS、GCB等)[11]。我国相继开展了针对C4气体合成、放电、分解、材料相容性等系统研究，并于2020年成功研制世界首台使用C4气体的环保型1000 kV特高压GIL样机[12]。
虽然寻找SF6替代气体的研究工作已经持续了数十年，但迄今仍未发现性能全面优于SF6或相当的环保绝缘气体，这是因为若将替代气体应用于高压电气设备，不仅需满足SF6气体所具备的三大基本功能(绝缘、灭弧、传热)，而且必须同时满足表 1所列举的6个维度的性能指标或近乎苛刻的约束条件。
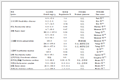表 1 SF6替代气体需满足的性能指标参数Table 1 List of the demanding requirements for the alternative gases to SF6
就已知的上亿种化合物而言，能够满足6大指标其中之一的可选气体分子，实际上数目众多，例如找到绝缘强度高于SF6的单质气体非常容易。但是，能够同时满足2个维度指标要求的可选气体分子数目则迅速呈指数减少，每增加1个维度，可选分子数目常表现为数量级削减，完全满足所有指标要求的单质气体至今尚未发现。例如，全卤代烷烃(PFCs)化合物的绝缘强度普遍高于SF6，但其GWP一般在5000~12 000之间，不足够环保，且分子尺寸增大毒性亦逐渐增强。全氟己酮(C6)的绝缘强度高约为SF6的3倍，比空气高近1个数量级，GWP=1且无毒，但其沸点高达49 ℃，室温下呈液态。虽然减小分子尺寸可降低沸点，例如C4F8O的沸点下降至0 ℃，但其毒性亦增强至半致死浓度LC50 = 200×10–6，同时绝缘强度也显著降低。环保型HFOs制冷剂的GWP普遍较低(< 10)，同等压力下绝缘强度可达到SF6的80%~90%，但液化温度仍较高，且不饱和键导致化学稳定性降低，在特定条件(例如微水、微氧等)下易分解、易燃、易爆，放电或电弧条件下则出现严重积碳现象。
由此可见，替代气体所需满足的各维度指标之间相互关联并相互制约。绝缘强度较高的气体，其液化温度普遍较高，二者存在一定的线性相关。其它指标参数之间也存在类似的相关性，譬如分子的稳定性与GWP，越稳定的分子越不易在大气中降解，必然导致大气寿命越长、GWP越高。因此，只有合理调控分子结构，使得气体各指标参数之间可以相互妥协(trade-off)，从而获得最优解，才有可能发现综合性能最优的SF6替代气体。单纯依靠试错试验实现结构–性能调控，效率低且不现实。建立多维度性能指标的构效关系模型，从理论上准确预测与评估气体的宏观性能，成为筛选与设计SF6替代气体行之有效的最佳方案。
2 SF6替代气体的多维度构效关系模型
关于SF6替代气体实验与理论研究进展的综述已有较多文献报道[3-6]，其中Wang等人综述了替代气体的构效关系与分子设计的现状，但仅限于绝缘强度单一维度模型[6]。显然，新型绝缘气体分子筛选与设计亟需绝缘、液化、环保、安全性等多维度构效关系模型的支撑。与已有综述不同，本文重点讨论了气体绝缘强度、沸点、GWP、毒性、可燃性、灭弧特性共6个维度构效关系模型的思想与进展。针对绝缘强度构效关系模型，则从描述符和训练数据库入手，侧重讨论各经验模型的适用范围与优缺点。
2.1 绝缘强度(Er(SF6)=1)构效关系模型
气体的绝缘强度存在多种实验数据表征方式，一般常采用击穿电压(UB)和临界击穿场强(E/N)lim两种物理量表示，其中UB包括交流和直流击穿电压。因UB数据受电场均匀度、气体压力P、电极间距d、电极材料等测量条件的影响，衡量SF6替代气体的绝缘强度常采用该气体的击穿电压U,gasUB,gas与相同实验条件下SF6的击穿电压U,S6UB,SF6的比值，即
E=/Er=UB,gas/U,U,UB,SF6 (1)
气体分子结构与绝缘强度的关联特征一直是电气领域基础研究的热点。早在19世纪40年代，人们就开始思考气体绝缘强度与分子结构或性质的内在关系，折射率、分子量、密度、紫外吸收光谱、原子化焓、沸点、电负性、电离能、电子亲合能等分子性质均被用来定性描述或解释气体的绝缘性能。虽然这些分子的物理性质与绝缘强度有关，但研究表明二者并不一定存在显著相关，定量预测气体的绝缘强度需要严格的构效关系模型。附表 A2列举了近年来具有代表性的气体绝缘强度的若干构效关系模型。
首个真正意义上能够预测任意气体绝缘强度的构效关系模型出现在1982年[13]。Brand系统研究了41种气体的绝缘强度随电离能和极化率的变化关系，2种描述符参数均取自标准数据表的实验值。值得指出的是，Brand提出了构效关系模型所用绝缘强度实验值(训练集)的3条筛选标准，即：均匀场(特定形状的放电电极)；统一的pd；不同来源的测量数据具备一致性。虽然只采用了2个描述符，但该模型的相关系数已经达到R=0.91，表明气体绝缘强度的确与电离能和极化率存在较为密切的依赖关系。然而，该模型的精度并不高，例如c-C6F12的预测值3.08比实测值2.35偏高31%。更重要的是，某些气体与SF6的相对绝缘强弱预测有误，包括CF3Br、CF2=CFCl、C3F8、C3F6等分子，理论绝缘强度均高于SF6，与实测值恰恰相反。特别是C3F8气体，实验绝缘强度仅为SF6的94%，但模型预测值高达SF6的2倍。显然，采用Brand模型筛选SF6替代气体或将导致不合理结果。后来Lin等人[14]和Zhang等人[15]相继改进了Brand的模型，采用理论计算的电离能和极化率参数，并使用了不同的训练数据库，但效果并没有显著改善。
2004年Meurice建立了43种气体的绝缘强度构效关系模型[16]，采用分子积分吸收强度作为唯一描述符，相关系数为R=0.85。首次采用密度泛函理论(DFT)方法，在BLYP/DNP理论水平优化气体分子结构并计算吸收光谱，从而开启了应用量子化学方法直接计算绝缘强度的先河。然而，该模型的相关系数偏低，部分气体的预测值比实测值偏低将近40%，且绝缘强度的相对次序亦难以保证。
2013年Rabie等人采用DFT-BP86理论方法，系统研究了绝缘强度与各种分子结构描述符的定量关系[17]，包括极化率α、偶极矩μ、垂直电离能εiV、绝热电离能εiа、垂直电子亲合能εаV、绝热电子亲合能εаа、HOMO-LUMO能隙ΔEgаp等，联合分子量Mω、电子数Ne参数，分别为极性(48种)和非极性(19种)分子建立了最优构效关系模型，相关系数分别为0.84和0.96，对非极性分子的预测稍优于极性分子。需要指出的是，该模型虽然采用了较为复杂的描述符和拟合函数(表3)，但其参数组合方式明显缺乏物理意义，仅仅采用最小二乘法得到了数学最优解。
2016年Zhang等人采用DFT−M06−2X理论方法计算气体分子的极化率和电子亲合能，通过线性回归，得到24种气体绝缘强度(数据未明确)的构效关系表达式[18]，此2参数模型的相关系数仅为0.78，稍逊于Brand的2参数模型。
2019年Chen等人采用B3LYP方法计算了37种气体的电离能εi、电负性χ、分子直径Dw参数，通过多元非线性拟合得到绝缘强度预测模型[19]，相关系数为0.95，但对于非极性或弱极性分子的预测结果较差，甚至无法正确定性预测不同气体的相对强弱。
2017年Yu等人发现电子–分子、分子–分子相互作用是决定气体绝缘强度的物理本质，首次提出采用静电势描述符构建气体绝缘强度的构效关系模型[20]。基于电子数密度和静电势的相互作用性质函数(GIPF)方法能够用于预测化合物的各种宏观理化特性，且各描述符均可采用量子化学计算方法优化分子结构
，取电子密度为0.001 au的等值面构建分子表面，计算表面上每一点的静电势U(r)，即：
U(r)=∑A−∫U(r)=∑AZA|RA−r|−∫ρ(r′)dr′|r−r′| (2)
式中：ZA为核电荷；RA为原子坐标；ρ(r')为电子密度。然后计算各种能够反映分子结构、形貌、静电相互作用的描述符，包括：分子正、负静电势的分表面积As+、As−和总表面积As；正、负静电势的平均值Vs+、Vs−和总平均值Vs；表面静电势的正、负方差σ2+σ+2、σ2−σ−2和总方差σ2totσtot2；正、负静电势的平衡度v=σ2+σ2−/(σ2tot)2v=σ+2σ−2/(σtot2)2；表示电荷分离程度或局域极性的静电势平均偏差Π；分子结构拓扑参数椭圆度Ovаl、分子体系V、分子量Mw等。经多次改进[21]，最终建立了5参数构效关系模型，相关系数R=0.993、平均绝对偏差DMA=0.061、标准偏差σ=0.080、最大绝对偏差δmax=0.28，结果明显优于其它构效关系模型。值得一提的是，该模型不仅能够较为准确地预测任意气体的绝缘强度，而且所采用的描述符均具有明确的物理意义，可以揭示绝缘强度随分子结构的演变规律：绝缘强度主要取决于分子总表面积、电荷分离程度、约化正电势密度3个正贡献量和局域极性1个负贡献量，从而为合理化设计高绝缘性能的分子结构奠定了理论基础。
随后，一些研究组开始使用静电势参数描述绝缘强度。例如，Sun等人以静电势描述符(特别是As+)为基础，并结合分子电性质参数、分子轨道等，建立了绝缘强度的人工神经网络(ANN)和随机森林(RF)模型[22]。从相关系数和均方根误差来看，RF模型优于ANN模型。You等人采用静电势参数，结合电子总能量，建立了不同pd范围的气体AC击穿电压与分子结构参数的构效关系模型，并获得了较好的预测结果[23]。
构效关系模型具有诸多优点：所有输入参数均可由DFT直接计算获得，根据模型表达式可快速判断绝缘强度，定量比较任意气体与SF6的绝缘性能，适合高通量筛选等。然而，任何经验性的构效关系模型都或多或少存在缺点或短板，主要包括以下两点：
1）理论模型均强烈依赖于所选择的训练集，即绝缘强度的实验数据库，包括气体分子类型、数量、测量方法等，原则上只有完全统一测量条件下的实验数据才能用作建立构效关系模型的训练集。然而，实际上绝缘强度实验数据相当分散，这是因为气体的击穿电压、临界击穿场强等实验数据均受测量条件的严重影响，即使微小的实验条件差异，气体的绝缘强度也会出现截然不同甚至相反的测量结果。因此，建立合理的构效关系模型，绝不能简单地将实验数据罗列，亦非越多越好，而必须将已有实验数据进行细致甄别，只能使用那些可以用于模型训练的实验数据。因此，训练集不是实验数据的简单集合，并非所有的实验数据都能用于训练替代气体的构效关系模型。例如，即使最简单的SO2分子，文献所报道的绝缘强度分散在0.5~1.5范围，换言之，SO2与SF6的绝缘强度孰高孰低迄今仍未明确。显然，诸如此类的气体分子不应包含在训练数据库中，贸然使用必将导致错误结论。
事实上，目前仅有Brand和Yu等人在优化构效关系模型时对已有实验数据进行了细致筛选。根据SF6替代气体的特点，绝缘强度的实验数据必须至少满足4点要求才能用于模型训练研究：(1)实验气体必须包括SF6，并以其为内标衡量其它气体的绝缘强度；(2)所有测量需基于同一实验条件，至少应使用相同的气体压力p与电极间距d，即pd值一致，并尽可能使pd较大；(3)采用均匀场或近似均匀场，避免非均匀场中气体放电的非线性现象；(4)在误差范围内，不同来源的实验测量需自洽或一致。
2）描述符的选择具有一定的经验性。原则上同一实验数据库可以使用完全不同的描述符优化构效关系模型，导致理论模型的非唯一性，不仅极大限制了模型的使用范围，任何构效关系模型只能在有限范围(比如某些特定类型的化合物)内适用，难以普适；同时极大弱化了理论模型所应有的物理意义。此外，采用具体函数表达式的构效关系模型尚能揭示一定的物理规律，机器学习与人工智能类的理论模型(如人工神经网络)虽然自动化程度高，但往往仅限于数据挖掘，甚至无法明确描述符在构效关系模型中所反映的物理本质。
为了克服以上构效关系模型的固有缺陷，最近Hou等人提出了预测气体绝缘强度的官能团加和(GA)方法[24]，将绝缘强度按比例分配到分子的各种原子或官能团上，优化分配系数，从而实现绝缘强度的快速预测。已设计的官能团类型包括：C—X，S—X，N—X，CX2和CX3(X = F, Cl, Br, I)、C(芳香族sp2杂化、非芳香族sp、sp2和sp3杂化、环状sp3杂化)、C≡N、SCN、C=O、S=O、S(=O)2、N(=O)2、N=S、C=N等。经检验，优化GA模型给出的65种气体的绝缘强度与实测值的相关系数达到0.99，平均绝对偏差仅为0.066，
平均相对偏差为6.3%，整体优于前期构效关系模型。除了能够快速、准确预测未知气体的绝缘强度之外，GA方法的更大价值在于能够揭示绝缘强度随分子结构的变化规律，特别是官能团成键特征与加和效率的关系，为设计具备更优绝缘性能的气体分子结构指明了方向。
基于分子结构参数预测绝缘强度，除了采用构效关系模型之外，还可以根据等离子体动力学理论，求解Boltzmann方程获得任意气体(包括混合气体)的临界击穿场强。电子在6维相空间的分布函数f满足方程：
∂f∂t+ν⋅∇f−E⋅∇νf=C(f)∂f∂t+ν⋅∇f−E⋅∇νf=C(f) (3)
式中：ν为电子速度；E为电场强度；C(f)为各种碰撞截面函数(包括激发、吸附、电离等)。精确求解Boltzmann方程非常困难，通常采用两项或多项近似方法。放电气体各组分的碰撞截面是确定反应系数的关键输入参数，但目前只有少数气体分子的完整实验数据，例如SF6、CxFy等常见分子。Zhao等人通过两项近似Boltzmann方程[25]，计算了SF6气体在0.4 MPa和0.8 MPa压力下、300~3000 K温度范围内的临界击穿场强(E/N)lim，理论计算与实验测量结果相符。随后采用同样方法计算了SF6/CF4、SF6/CO2、SF6/O2、SF6/CH4、SF6/C2H6和SF6/CHF3等一系列混合绝缘气体在300 K下的(E/N)lim，获得了混合比、压力等设计参数对气体绝缘性能的影响规律。Zhao等人采用同样方法分析了CF3I/CO2、CF3I/N2混合气体的协同效应，计算结果与工频电压下的绝缘特性实验值基本相符[26]。
当缺乏气体关键组分的截面数据时，则需开展SSD实验测量或由经验参数近似，亦可采用Deutsch-Mark理论，结合量子化学计算的分子轨道信息，模拟气体组分的截面参数。Wang等人计算了H2O、C3H6O、C5F10O、C6F12O等分子的总碰撞电离截面，与实验结果相符，并发现自然原子轨道最适于Deutsch-Mark理论模拟[27]。
2.2 液化温度构效关系模型
气体的液化温度T与饱和蒸气压p有关，一般采用Clausius-Claperyron方程描述气体的蒸气压-液化温度曲线，即：
lnp=−ΔRT+Clnp=−ΔHvapRT+C (4)
式中：ΔHvap为蒸发焓；R和C分别为理想气体常数和积分常数。饱和蒸气压p = 101 325 Pa所对应的液化温度即为化合物的正常沸点Tb。可以看出，一旦确定Tb和ΔHvap，即可计算任意压力下气体的液化温度。作为常规理化参数，文献中积累了大量化合物的Tb实验数据，但专门针对绝缘气体特别是含氟化合物沸点的构效关系模型并不多见。Liang等人提出了一种预测全氟化合物沸点的官能团加成方法[28]，并引入分子极化率参数α作为校正项，即：
Tb=aln(∑nT)+bαTb=aln(∑niTb, i)+bα (5)
基于全氟酮与线性/支化、环状等各类全氟烃化合物共27种，采用—CF3、> CF2、> CF—、c-CF、c-CF2、> C=O共6种官能团并优化其沸点贡献比例Tb, i，得到参数a=103.3，b=0.678。模型相关系数R2 =0.997，理论与实验沸点的均方根误差为3.9 ℃，最大偏差为6.8 ℃。
化合物的沸点主要取决于分子间相互作用，中性分子之间一般以短程范德华力和长程静电作用力为主。因此，基于分子静电势的描述符常被用于建立沸点、蒸发焓、临界温度等构效关系模型。Murray等人采用量子化学方法计算了3个静电势统计参数：总表面积As、表面静电势总方差σ2totσtot2、正/负静电势平衡度ν，获得了99种有机化合物沸点的构效关系模型[29]，即：
T=aA+bνσ2−−−−√+cTb=aAs+bνσtot2+c (6)
相关系数R=0.949。2017年，Yu等人试图将此模型推广应用到SF6替代气体的沸点预测[20]。以54种替代气体的沸点实验数据为基础，采用与Murray同样的函数关系式重新拟合，发现所得模型的相关系数降为0.84，沸点温度平均偏差高达36.5 ℃。例如，计算的SF6沸点高达13 ℃，远远偏离实验值−64 ℃。由此可见，Murray等人的模型中所用描述符并不能正确反映绝缘气体液化温度随分子结构的演变规律。Yu等人采用静电势平均偏差(Π)替换方差σ2totσtot2参数，并引入分子硬度参数η，构建了针对绝缘气体沸点的全新构效关系模型[20]，即：
Tb=125.3Π2−143.2A−1s+194.7η−+27.0Tb=125.3Π2−143.2As−1+194.7η−13+27.0 (7)
其中η定义为最高占有分子轨道(HOMO)和最低空轨道(LUMO)能量差的一半。因此，该模型的所有描述符均可由量子化学计算直接得到，相关系数R2 = 0.985，标准偏差为8 ℃。此3参数模型的成功主要源于同时兼顾分子静电势参数与电子性质参数，其中由分子轨道所决定的硬度参数贡献占50%以上。
最近，Sun等人基于66种SF6替代气体的沸点实验数据[22]，使用7个描述符建立了沸点的ANN和RF模型，相关系数分别为0.951和0.966，标准偏差16.6 ℃和12.4 ℃，RF模型的预测精度比ANN稍高。
与绝缘强度不同，气体沸点的实验数据一般较为准确可靠，目前基于构效关系模型得到的理论与实验的相关性普遍较好，但预测的Tb绝对偏差仍然较大。鉴于液化温度在替代气体分子筛选中的重要性，为了避免漏选、错选，沸点预测精度需达到±1~2 ℃范围。因此，目前关于沸点的构效关系模型仍有较大的改进空间，同时需要发展精准预测SF6替代气体沸点的新理论方法。
分子动力学模拟(MD)方法或巨正则系综Monte-Carlo(GEMC)方法可以模拟单质化合物或混合物的气−液相平衡，获得饱和蒸气压随温度的变化曲线，从而直接得到沸点和蒸发焓。与仅依赖单分子结构的构效关系模型不同，MD或GEMC模拟计算强烈依赖于分子间相互作用势，即力场(force field)。文献中报道了大量模拟有机和无机化合物的力场模型，诸如COMPASS、UFF、NERD等，通用性较好、应用广泛。但是，现有力场并不适用于SF6及其替代绝缘气体。例如，因力场参数缺失，在分子模拟领域最受欢迎的COMPASS力场甚至无法正确描述SF6的分子结构，即使改进后的COMPASS-Ⅱ/Ⅲ力场也难以正确描述SF6的理化性质。因此，开展替代气体的MD或GEMC模拟计算之前，必须首先考察力场的可靠性，结合量子化学计算验证力场描述分子间相互作用的准确性，确保模拟结果的合理性。
通过拟合密度、粘度、表面张力等若干实验数据，2007年Olivet等人建立了SF6气体的力场模型[30]，理论计算的蒸气压–温度曲线、沸点、临界性质、输运特性等均与实验一致。最近，Hou等人基于各种高精度量子化学理论方法计算的C4分子间相互作用势能，建立了适用于全氟腈化合物的全原子力场[31]。该力场模型预测的两C4分子间相互作用随N—N间距的能量变化曲线与各种量子化学计算方法得到的数据相符。随后，采用GEMC方法模拟了C4的气–液相平衡，获得了饱和蒸气压P随温度t的变化关系，如图 2所示，理论计算结果与已有实验数据相当一致。根据Claussius-Clapeyron方程计算C4的沸点为−5.3 ℃，与实验值−4.7 ℃相比，仅偏低0.6 ℃，完全满足分子设计与筛选的需求。同时，采用MD方法模拟了C4的临界性质和扩散系数、粘度、介电常数、热导系数等输运特性，为C4的电气应用仿真提供理论依据。此理论方法可以推广应用到其它SF6替代气体液化温度的精确模拟研究。
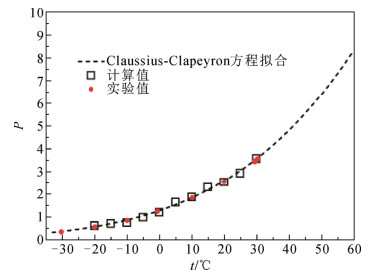图 2 不同温度下C4的饱和蒸气压Fig. 2 Temperature-dependent vapor pressures of C4
2.3 GWP构效关系模型
GWP是IPCC(intergovermental panel on climate change)出版的首次报告中所定义的物理量，旨在用于表征不同温室气体对全球气候变化影响程度的差异。GWP概念在学术界一直饱受争议，但工业界常用于环境问题相关的决策。
IGWP指一次性排放(pulse emission)单位质量气体在设定时间窗口期th内辐射力(radiative forcing, RF)FR的积分，即
I=∫0FdtIGWP=∫0thFRdt (8)
IGWP绝对值的单位为W·m−2·kg−1·a。在实际应用中，IGWP常表示为无量纲的相对值，一般以CO2气体(FR,CFR,CO2)为参考标准，即：
IGWP=dt/dtIGWP=∫0thFRdt/∫0thFR,CO2dt (9)
IPCC报道th分别为20、100、500 a的IGWP数据。国际上较为流行的IGWP数据(例如在Kyoto Protocol中)均取th=100 a时间窗口期。如果以辐射效率(radiative efficiency, RE，即单位大气浓度的RF)ηRE表示，GWP可由下式计算：
IGWP=τ(1−)W/IGWPIGWP=ηREτ(1−e−thτ)W/IGWP,CO2 (10)
文献中常将CO2的IGWP归一化，即定义CO2的IGWP,CIGWP,CO2=1。式中W为分子量，τ为大气寿命，其数据来源有3种：一是直接气象观测气体浓度随时间的变化；二是采用温室实验装置模拟气体降解速率，测量气体在典型大气条件下的存活时间；三采用量子化学方法模拟化合物的大气传输、辐射、降解机理，根据过渡态理论计算降解速率及大气寿命。值得指出的是，将气体的大气降解近似为指数衰减函数仅适用于长寿命气体。对于化学活性较高的气体分子，其降解速率与输运速率相当，在大气层内还来不及形成均相分布即被完全降解。因此，短寿命气体分子的GWP依赖于具体区域、时间等因素，严格意义上不再适用GWP概念。IPCC和WMO(World Meteorological Organization)对此类短寿命气体的GWP一般不予报道，但是学术界经常延用GWP代表温室效应的上限值。
化合物的辐射效率取决于其红外吸收截面，实验较易测量，理论计算也相对较为简单。2008年Young等人提出了一种快速估算氟代醚化合物辐射效率的构效关系模型[32]。依据11种气体的实验值和154种气体的量子化学计算值，采用官能团加和方法，仅根据分子结构即可迅速预测气体的RE数据，相对偏差小于25%。但是，该模型仅限用于氟代醚化合物，无法外推到其它类型的SF6替代气体。更为普适的方法为1995年Pinnock提出的振动频率(波数)依赖的RE计算模型[33]，仅需将气体的红外吸收截面与“Pinnock曲线”相乘，即可直接得到RE数据。目前几乎所有的量子化学方法(包括DFT)均可预测任意气体分子的红外吸收光谱，且精度较高。2012年Kazakov等人采用半经验量子化学方法PM6计算了100多种潜在制冷剂气体分子的红外吸收光谱[34]，振动频率采用0.9069标定因子，理论计算的RE与实验结果相符，对数均方根偏差仅为1.84，能够满足分子结构虚拟筛选的要求。2016年Betowski等人考察了量子化学方法与基组对估计RE的影响，使用各种DFT(B3LYP、PBE、MN12-L等)和MP2方法计算了235种气体的RE，理论值与实测值的平均绝对偏差在0.013~0.208范围内[35]。
与辐射效率截然不同，关于气体大气寿命的实验测量或理论计算颇具挑战性。如前所述，即使最成熟的SF6气体的大气寿命，实验数据分散在580~3200年范围，至今仍无法取得一致结果。这是因为化合物的大气降解过程非常复杂，包含化学降解(与OH、O3、Cl、NO3等自由基反应)、光降解、水解(沉积、雨水冲刷、海洋降解等)、电子碰撞解离等众多机理。
在大气化学中，OH自由基常被称为大气“洗涤剂”，大多数气体的降解过程以与OH反应为主。文献中积累了大量气体与OH反应的实验以及相关反应机理的理论研究，并发展了各种简便预测反应速率常数(kOH)的理论方法，其中应用较为广泛的是Atkinson等人提出的官能团加和模型[36]，即：
k=k+k+k+kkOH=kabs+kadd+karom+kNSP (11)
式中：kabs为抽提C—H和O—H基团上H原子的速率常数；kadd为OH加成到C=C双键和C≡C三键上的速率常数；karom为OH加成到芳环上的速率常数，kNSP为OH与含N、S、P等官能团的反应速率常数。每一种气体的每一个k值分解为组成该分子的官能团贡献因子ki和取代因子Fi，其数值通过拟合298 K温度下485种气体与OH自由基的反应速率常数确定。例如，CH3基团的k=1.36×10−12 cm3·s−1，CF3官能团的取代因子为0.071。采用该模型预测速率常数，超过90%反应的理论速率常数与实验值的偏差均在2倍以内。遗憾的是，对于卤代有机化合物(特别是卤代烷、烯、醚等)，误差较大。鉴于多数此类卤代分子具有成为SF6替代气体的潜力，显然该模型必须改进后才能发挥作用。
2015年Allison等人采用人工神经网络(ANN)方法，考察了791个气体分子与OH自由基的反应[37]。基于分子的2D结构确定所包含的原子类型与化学键类型，并以键长、键角的类型与个数共109个描述符(例如CH4分子包含4个C—H键和6个H—C—H键角)，优化ANN模型预测的理论速率常数与实验值的平均相对误差约为12%。
根据反应速率系数kOH以及OH自由基的年平均粒子数密度(n(OH)=106 cm−3)，即可获估算大气寿命τ = 1/kOH·n(OH)，结合RE即可预测GWP数据。2012年Kazakov等人计算了100余种潜在制冷剂的GWP[34]，如图 3所示。虽然GWP分布范围很宽，跨越4个数量级，但理论预测值与实验值的相关性较好，对数均方根误差为3.0，已被用于新型环保制冷剂的虚拟筛选研究。
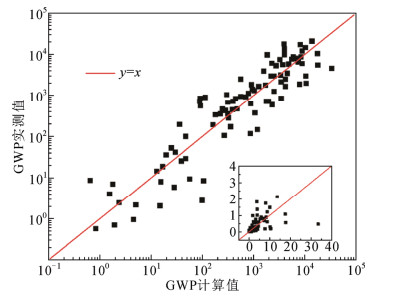图 3 若干潜在制冷剂的GWP值对比(插图为正常坐标)Fig. 3 Comparison of estimated and reported logarithmic GWP for refrigerants. The insert is in normal scale
然而，由于采用GWP对数形式拟合，图 3所展示的相关性事实上并非可靠，表面上的高相关容易造成误解。采用正常坐标的GWP对比如图 3中插图所示，很明显GWP的计算值与实测值存在显著差异，很多分子的GWP远远偏离了实验值。例如CF3I的GWP理论预测值高达6200，成为非环保气体，这与实验值GWP = 5截然相反，表明该构效关系模型并不足够准确，用于筛选环保气体将可能导致定性错误。究其原因，主要问题应归于大气寿命的高度不确定性，除了与OH自由基反应之外，还应考虑更多的大气降解过程，建立能够准确预测化合物大气寿命的构效关系模型至关重要。
2.4 安全性能构效关系模型
鉴于高压电气设备的特殊的工作条件与运行环境，绝缘气体的安全性能至关重要，特别是毒性和可燃性2个指标。不仅需评估绝缘气体本身的毒性与可燃性之外，还需考虑气体因放电或热分解产生的各种产物碎片的安全特性。因此，与绝缘强度、液化温度等指标相比，SF6替代气体的安全特性评价显然更为复杂。
毒性是一个相对较为模糊的概念，文献中存在各种各样的定义或标准，而不同定义和测量方法给出截然不同的毒性表征参数。ACGIH(American Conference of Govermental Industrial Hygienists)建议采用TLV(threshold limit values)和BEI(biological exposure indices)衡量化合物的毒性，其中TLV包括4类数据，即：工作暴露限值(time-weighted average，TWA，每天8 h、每周40 h的工作暴露限值)、15 min工作暴露限值(short-term exposure limit，STEL)、设备表面浓度限值(surface limit，SL)、任何场合工作暴露不能超过的限值(ceiling，C)。例如，SF6气体的TWA为1000×10–6，而SO2F2气体的TWA和STEL分别为5×10–6和10×10–6，SF4气体的C为0.1×10–6。遗憾的是，不同来源的各种毒性数据通常相差较大。Oberg等人指出现有发布的化合物毒性参考标准中的数据严重不一致[38]，如AEGL(acute exposure guidance levels)和ERPG(emergency response planning guideline)，揭示了气体毒性的高度复杂性，给SF6替代气体的毒性构效关系模型研究带来了巨大挑战。
Brand尝试采用气体的最大允许浓度(MAC)毒性数据[13]，以极化率和电离能为描述符建立毒性与分子结构的构效关系模型。由于实验数据匮乏且过于分散，并没有得到有实用价值的定量关系式。最近Yu等人以15种SF6替代气体的MAC毒性数据为基础，定义各气体与SF6的相对毒性(Cr)，发现可以采用与绝缘强度、液化温度构效关系模型相类似的静电势描述符建立毒性构效关系模型[39]，初步研究结果如图 4所示，即：
lnCr=37.03(νσ2)−−0.056Π−3−23.24ρA+lnCr=37.03(νσtot2)−12−0.056Π−3−23.24ρeAs,r+ (12)
然而，由于采用GWP对数形式拟合，图 3所展示的相关性事实上并非可靠，表面上的高相关容易造成误解。采用正常坐标的GWP对比如图 3中插图所示，很明显GWP的计算值与实测值存在显著差异，很多分子的GWP远远偏离了实验值。例如CF3I的GWP理论预测值高达6200，成为非环保气体，这与实验值GWP = 5截然相反，表明该构效关系模型并不足够准确，用于筛选环保气体将可能导致定性错误。究其原因，主要问题应归于大气寿命的高度不确定性，除了与OH自由基反应之外，还应考虑更多的大气降解过程，建立能够准确预测化合物大气寿命的构效关系模型至关重要。
2.4 安全性能构效关系模型
鉴于高压电气设备的特殊的工作条件与运行环境，绝缘气体的安全性能至关重要，特别是毒性和可燃性2个指标。不仅需评估绝缘气体本身的毒性与可燃性之外，还需考虑气体因放电或热分解产生的各种产物碎片的安全特性。因此，与绝缘强度、液化温度等指标相比，SF6替代气体的安全特性评价显然更为复杂。
毒性是一个相对较为模糊的概念，文献中存在各种各样的定义或标准，而不同定义和测量方法给出截然不同的毒性表征参数。ACGIH(American Conference of Govermental Industrial Hygienists)建议采用TLV(threshold limit values)和BEI(biological exposure indices)衡量化合物的毒性，其中TLV包括4类数据，即：工作暴露限值(time-weighted average，TWA，每天8 h、每周40 h的工作暴露限值)、15 min工作暴露限值(short-term exposure limi,STEL)、设备表面浓度限值(surface limit，SL)、任何场合工作暴露不能超过的限值(ceiling，C)。例如，SF6气体的TWA为1000×10–6，而SO2F2气体的TWA和STEL分别为5×10–6和10×10–6，SF4气体的C为0.1×10–6。遗憾的是，不同来源的各种毒性数据通常相差较大。Oberg等人指出现有发布的化合物毒性参考标准中的数据严重不一致[38]，如AEGL(acute exposure guidance levels)和ERPG(emergency response planning guideline)，揭示了气体毒性的高度复杂性，给SF6替代气体的毒性构效关系模型研究带来了巨大挑战。
Brand尝试采用气体的最大允许浓度(MAC)毒性数据[13]，以极化率和电离能为描述符建立毒性与分子结构的构效关系模型。由于实验数据匮乏且过于分散，并没有得到有实用价值的定量关系式。最近Yu等人以15种SF6替代气体的MAC毒性数据为基础，定义各气体与SF6的相对毒性(Cr)，发现可以采用与绝缘强度、液化温度构效关系模型相类似的静电势描述符建立毒性构效关系模型[39]，初步研究结果如图 4所示，即：
lnCr=37.03(νσ2)−−0.056Π−3−23.24ρA+
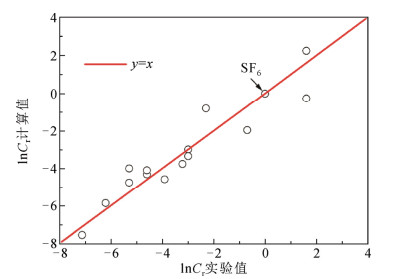图 4 SF6替代气体毒性构效关系模型(Cr, SCr, SF6=1)Fig. 4 Structure-activity relationship model for the toxicity with respect to SF6 (Cr, SCr, SF6=1)
该模型的相关系数为0.89，标准偏差为0.86。可以看出，气体毒性、绝缘强度、液化温度3个维度之间存在某种内在关联，通过调整分子结构，改变三者共有的静电势描述符，则有望设计或筛选出毒性低、绝缘强度高、液化温度低的新型替代气体。
实践证明，新型环保绝缘气体与制冷剂、灭火剂常有交集，目前试验筛选出的绝缘气体多为含碳有机分子，诸如氢氟碳HFCs、氢氟醚HFEs、氢氟烯烃HFOs等。这些有机化合物的燃烧特性是决定其是否适用于高压电气设备的关键因素。一般认为分子中含氟越多，可燃性越低。定义化合物中F原子与H原子的相对占比FR=nF/(nH+nF)，若FR超过一定限值，则该物质不可燃。Kondo等人系统研究了120种饱和含氟化合物的可燃性，发现绝大多数不可燃气体的FR > 0.625，可作为判断气体是否可燃的简单标准。例如：CH3F(FR=0.25)、CH2F2(FR=0.5)属于可燃气体，而CHF3(FR=0.75)、CF4(FR=1)则不可燃，事实亦如此。进一步研究发现，除了FR值，可燃性与分子中F原子的分布状态也有关系[40]。针对74种HFCs、HFEs、HFOs气体，Kondo等人研究了燃烧上限值(U)和下限值(L)与分子结构的关联。定义表征U和L限值平均值的物理量F和G，即：
F=1−LU−−−−√F=1−L/LUU (13)
G=LU−−−√G=LU (14)
采用官能团加和方法，通过线性回归分析，获得了计算F和G值的构效关系模型：
F=p1(1+p2C1+∑i=312piRi)F=p1(1+p2C1+∑i=312piRi) (15)
G=C1(1+q1(M−32)+q2C1+∑i=38)G=C1(1+q1(M−32)+q2C1+∑i=38qiRi) (16)
其中p1~p12、q1~q8为拟合参数；M为分子量，其余为与分子结构有关的描述符，包括：C1(=0或1，是否含C原子)、Ri代表总不饱和度、官能团(醚氧、C—CF3、CHF=C、C—CF=C、CF2=C等)的特征贡献值。该模型对燃烧上限和下限的预测结果均表现较好，平均相对偏差分别为10.3%和12.9%。
Kazakov等人考察了468种化合物的燃烧下限L(单位kg/m3)与燃烧焓ΔHc(单位MJ/kg)的定量关系[34]。采用半经验量子化学方法PM6计算化合物的燃烧焓，最小二乘法拟合的结果为：
L=2.38ΔH−1.19L=2.38ΔHc−1.19 (17)
这表明燃烧下限与燃烧热为反比关系。该模型的对数均方根误差为1.24，显然仅数量级可靠，且只适用于正燃烧焓化合物，虽然通常认为ΔHc < 3 MJ/kg的物质基本不可燃。
除了采用燃烧上限或下限值定量表征化合物的可燃性之外，工业上普遍采用对可燃性进行分级的方式定性描述。例如ISO和ASHRAE标准将冰箱制冷剂的可燃特性划分为4个等级：A1(不可燃：0.1 MPa、60 ℃在空气中无火焰)，A2L(低可燃：0.1 MPa、23 ℃燃烧下限 > 3.5%(体积分数)或0.1 kg/m3，空气中燃烧速率 < 0.1 m/s，燃烧热 < 19 MJ/kg)，A2(可燃：燃烧速率 > 0.1 m/s，其余同A2L)，A3(易燃：燃烧下限 < 3.5%(体积分数)或0.1 kg/m3，燃烧热 > 19 MJ/kg)。Devotta等人考察了179种制冷剂(包括47种纯物质和132种混合物)的燃烧特性，采用C、H、N、O、F、Cl、Br、I原子个数、双键个数、H原子质量占比、分子量共11种描述符，建立了化合物可燃性级别的人工神经网络和随机森林模型[41]。除个别分子(如R-426A、R-472A、R-455A等)预测错误之外，基本上可正确预测化合物所属的可燃等级，与实测值相比，理论精度达到0.96以上。其中，C和H原子个数在ANN模型中占比最大，而氢原子质量比例在RF模型中的贡献更为显著。
2.5 灭弧特性
如前所述，灭弧是SF6替代气体除绝缘、散热之外应必备的关键特性。气体电弧是一种典型的热等离子体，涉及电磁场、气流场、温度场、辐射场等多场耦合的物理化学过程。气体的灭弧性能与绝缘强度有关，但并非直接相关。例如CO2气体的绝缘强度只有SF6的1/3，而CO2的电弧形态与电弧电压均与SF6较为接近。这与CO2气体的热分解特性有关：分解不仅能够吸收部分电弧热量，而且释放出大量自由带电粒子提高导热性能，从而在高温下体现出较好的灭弧性能。研究表明CO2气体是一种理想的灭弧辅助组分，将其与其他绝缘强、但灭弧差的气体按一定比例混合，可以有效提高混合气体的灭弧能力。
目前对于环保绝缘气体灭弧特性的实验与理论研究均非常匮乏。Xiao等人对环保绝缘气体的灭弧能力进行了系统分析[42]，发现常规气体难以满足大电流开断的灭弧需求，仅CF3I具有较好的应用前景，并建议针对气体的灭弧过程及分解特性开展研究，并提出采用添加剂抑制分解、调整灭弧特性的气体混合方案。Li等人对气体开关电弧物性参数计算及特性仿真的研究和应用进行了综述[43]，包括热动属性、输运系数、碰撞截面、热态临界击穿场强等与灭弧特性直接相关的影响因素。提出电弧磁流体动力学(magneto-hydro-dynamics, MHD)是研究电弧理论和特性控制、促进开关产品研发和优化设计的有效工具，但受限于电弧物性参数的相对匮乏，亟需开展针对新型SF6替代气体灭弧的实验测量和理论模拟方法。
文献中关于SF6替代绝缘气体灭弧性能的定量研究仅有少量报道。Lee等人采用临界恢复电压上升率(rate of rise of recovery voltage，RRRV)IRRRV衡量气体灭弧性能判据[44]，由此定义灭弧强度为：
I=d/dt=I/tIRRRV=dUr/dt=Z0dI/dt (18)
式中：Ur为临界恢复电压；Z0为阻抗。设置气体总压力0.6 MPa、开断电流I为10~20 kA、燃弧时间7~8 ms、Z0=450 Ω或225 Ω，系统考察了16种SF6替代气体单质与混合气体的灭弧性能，结果表明没有任何一种气体的灭弧性能超过SF6，表现最佳的为SF6/N2(75/25%)和CH4/CClF2CF3(50/50%)混合气体，灭弧强度约为纯SF6的85%。由此可见，与混合气体的绝缘协同效应相似，灭弧性能也存在协同效应。
对CF3SO2F/SF6混合气体的灭弧性能数据进行分析，采用协同效应表达式为：
A=A2+k(−)k+(1−k)Am=A2+k(A1−A2)k+(1−k)Carc (19)
式中：A1、A2分别为两种气体单质的临界恢复电压上升率；k为SF6混合比；Carc为灭弧协同效应常数。拟合结果如图 5所示。当Z0=450 Ω时，协同效应曲线拟合CF3SO2F气体的灭弧强度出现不合理结果−14；当Z0=225 Ω时拟合其灭弧强度为31。表明气体灭弧强度与绝缘强度虽然均存在协同效应，但协同机理应存在显著差异，若采用线性拟合则CF3SO2F的灭弧强度分别为44和37。总之，初步推测CF3SO2F气体的灭弧强度应不及SF6的50%，这可能与其复杂的分子结构以及分解途径有关，导致CF3SO2F的自恢复能力明显不如SF6。但是，CF3SO2F的绝缘强度约为SF6的1.4倍，表明绝缘强度高的气体其灭弧能力不一定强，灭弧与绝缘之间不一定存在必然联系。图 6将5种气体的灭弧性能与绝缘强度进行对比，很明显二者并不存在显著相关。遗憾的是，由于气体灭弧强度的实验数匮乏，尚不足以支撑建立可靠的灭弧性能构效关系模型。从图 6可以看出，已知气体基本出现在Ⅲ区(绝缘优、灭弧差)和Ⅳ区(绝缘差、灭弧差)，最理想的Ⅰ区(绝缘优、灭弧优)尚未发现任何分子。
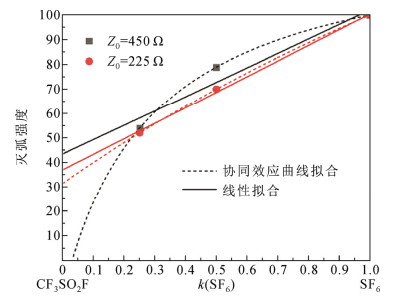图 5 CF3SO2F/SF6混合气体的灭弧强度(相对于纯SF6)Fig. 5 Arc interruption capability of the admixture of CF3SO2F/SF6
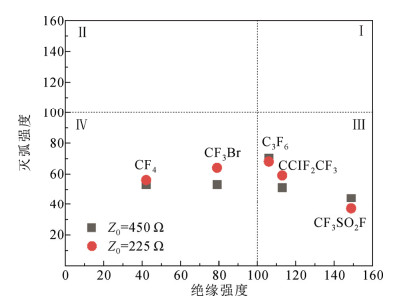图 6 典型气体的灭弧与绝缘性能对比(k(SF6)=100%)Fig. 6 Comparison of arc interruption capability to dielectric strength of some gases (k(SF6)=100%)
3 SF6替代气体筛选与分子设计方法
筛选潜在的环保绝缘气体，目前仍以从制冷剂、灭火剂、发泡剂中通过“试错”试验为主，因为此类新型工业制剂种类繁多，且对环保、液化温度、安全等性能也有同样需求，只需补充绝缘和灭弧测试试验，即可从中甄别出潜在的SF6替代气体。但是，电气试验昂贵且非常耗时，开展试验前的理论初筛研究将有助于提高创新效率与成功率。
发现新型SF6替代气体主要有2种理论方法，一是从已知分子数据库中进行高通量虚拟筛选，二是对气体分子结构进行合理化设计。无论是前者的“被动”式筛选，还是后者的“主动”式设计，都离不开预测气体性能的多维度构效关系模型。Li等人综述了基于DFT的SF6替代气体筛选方法，强调了构效关系模型、电子碰撞截面等参数在建立SF6替代气体综合性能评价体系方面的重要性[45]。
3.1 基于已知分子结构数据库的虚拟筛选
最新、最成功的SF6替代气体虚拟筛选研究由Kazakov等人[34]和Rabie等人[46]联合完成，其技术路线总结于图 7。Kazakov等人从PubChem(小分子及生物活性数据库)所列举的56203个分子出发，剔除有毒和不稳定的分子，依次采用GWP、燃烧下限(L)、临界温度(Tc)构效关系模型，基于3个维度筛选出1234个候选制冷剂分子，满足GWP < 200(环保)、L > 0.1 kg/m3(不燃)、Tc为300~550 K指标要求，主要为卤代烯烃、卤代醚和环状化合物。随后，Rabie等人引入了绝缘强度(Er)和沸点(Tb)2个维度的构效关系模型，试图从Kazakov等人筛选的1234种环保制冷剂中发现SF6替代绝缘气体。采用经济学中博弈论方法，由帕累托最优化(Pareto efficient：在没有使任何物理量变坏的前提下，使得至少一个物理量变得更好，直至不可能再有更多改进的余地为止)方法获得了141种潜在的SF6替代气体分子。排除具有安全隐患的化合物，最终从21种已实现商品化的气体中获得7种候选SF6替代气体，列于表 2，包括5种氢氟烯烃、1种氟代烷、1种氟代醇。
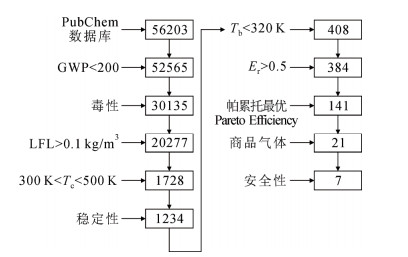图 7 环保绝缘气体分子的虚拟筛选技术路线Fig. 7 Protocols for the virtual screening of the eco-friendly insulation gases
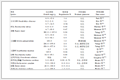表 2 Rabie等筛选的7种潜在SF6替代绝缘气体[46]Table 2 Seven replacement gases for SF6 from the computational screening by Rabie et al.
分析发现，用于虚拟筛选的GWP、L、Tc、Er、Tb的构效关系模型普遍存在较大误差，往往难以准确定量预测分子的性能，甚至定性比较也无法保证。例如Er和Tb的标准偏差分别高达0.35和28 ℃，构效关系模型预测C4分子的绝缘强度高达3.2，远高于实验值2.0。同时，毒性、可燃性等维度的筛选仅依据商用试剂标签，明显具有较高的不确定性。以上缺陷必然导致大量漏筛或错筛现象。根据PubChem数据库的最新记录，Rabie等人筛选的7种候选SF6替代气体中的6种已被重新标记为有毒、易燃、腐蚀或刺激物质，仅剩唯一(CF3)2C=CHCF3气体具备潜在替换SF6的可能。因此，针对新型环保绝缘气体的虚拟筛选研究仍需开展更精准、更细致、更深入的理论探索。
3.2 替代气体分子结构的合理化
设计以新型环保绝缘气体为目标，Yu等人提出了两种分子结构设计方法[47]：化学键杂化与官能团取代。经初步验证，该方法不仅能够从数据库中主动挑选出合适的已知气体，而且能够创造出未知的全新分子。
化学键杂化是指以若干母体分子为基础，将一部分特征结构按照某种设定的方式重新组合，形成全新化学键。与气体的简单物理混合不同，化学键杂化的分子可看作若干碎片按比例组合所形成的“化学混合”产物。结合构效关系模型进行组合设计，所得分子可自然具备绝缘强度高、液化温度低、GWP低等特点。以SF6和N2为例加以说明。SF6/N2混合气体的绝缘、液化、灭弧等性能较为优异，已被用于高压、特高压输电设备的绝缘介质，但其中仍含有相当比重的SF6。若将SF6的50%碎片(即SF3)和N2的50%碎片(即N原子)重新组合，则可以形成新型的S≡N三键，由此产生的SF3N分子“继承”了SF6和N2母体分子的优点：绝缘强度是SF6的1.3倍、液化温度−27 ℃，S≡N三键不仅使其GWP远低于SF6，稳定性亦得到提高，初步实验研究证明了SF3N及其主导的混合物均表现优秀的绝缘性能。Yu等人设计出CF3SO2F(CF4+SO2杂化)、CF3OCFO (CF4+CO2杂化)，CF3N=CF2(C3F6+N2杂化)等具有潜力的新型SF6替代气体，部分气体已开展了实验合成与绝缘测试研究，充分表明了理论分子设计的可行性和有效性。
官能团取代是指将母体分子结构中的部分原子或基团用具有特定功能的官能团取代或重排，从而形成新分子结构。例如，氰基C≡N官能团的电负性强、活性高，对提高绝缘强度，降低GWP非常有效。将全氟丙烷(C3F8，CF3—CF2—CF3)中间C原子上的1个F原子用CN基团取代，则得到3M公司开发的七氟异丁腈(C4)分子，显著降低C3F8的GWP的同时将绝缘强度提高约1倍。基于绝缘强度和液化温度的官能团加和模型[46]，Hou等人发现SF5CN、NF2CN等分子亦兼具绝缘强度高、液化温度低以及环保特性，可作为新型SF6替代气体开展测试试验研究。
目前针对SF6替代气体的分子设计大多集中于Er和Tb两个维度。虽然在设计时考虑了降低GWP的某些策略(如引入不饱和化学键、活性基团等)，但并没有明确考虑GWP、毒性、可燃、灭弧等维度所对应的分子结构特征，亟待在现有构效关系模型的基础上进行扩维研究。基于多维度构效关系模型，图 8总结了发现新型SF6替代气体策略的技术路线，包含分子结构设计与性能评估、实验室合成与测试、工业制备与电气应用等，为加速SF6替代气体研发进程提供理论指导。
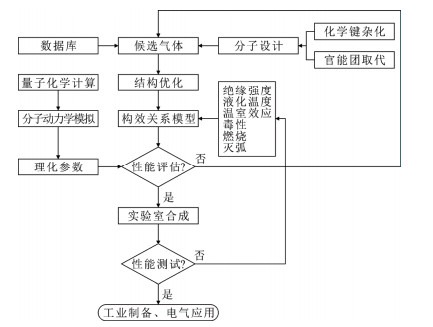图 8 新型SF6替代气体分子的发现策略Fig. 8 Proposed strategy for discovery of novel replacement gases for SF6
4 结论
采用多维度构效关系模型筛选与设计新型环保绝缘气体已取得了显著进展，但受制于SF6替代气体的苛刻要求，特别是各项必备性能参数之间的相互制约，对应的理论模型仍有较多不足，主要表现为：
1）模型严重依赖用于训练集的实验数据，其中：绝缘强度数据分散，完全统一实验条件下的绝缘数据相对较少；气体的毒性数据标准不一；灭弧性能数据缺少标准且严重匮乏等。
2）模型中描述符的物理图像不明，参数选择具有一定随意性；气体的宏观特性与微观分子结构的关联仍未完全理清。
3）各维度之间的相关性及相互制约关系仍不明，导致环保绝缘气体分子的创新与发现也难以突破。
鉴于研发新型环保绝缘气体的巨大挑战性，只有整合分子结构设计与性能评估、实验室合成与测试、工业制备与电气应用等一系列关键技术，实验与理论相辅相成、循环迭代，才有可能突破目前SF6替代气体的研究瓶颈，挑战与机遇并存。亟需进一步开展的实验与理论研究包括：
1）基于完全统一实验条件，测量各种潜在SF6替代气体的击穿电压或临界击穿场强，建立训练绝缘强度构效关系模型所必需的实验数据库，揭示气体绝缘强度随分子结构的演变规律。
2）基于量子化学方法，计算电子与气体分子的相互作用，建立原位模拟电子碰撞电离、电子附着与解吸等微观机理以及动力学过程的先验性理论方法，揭示气体放电现象的物理与化学本质。
3）开发通用型、高精度力场模型，采用分子动力学与Monte-Carlo方法模拟电负性气体的气–液相平衡状态，建立评价替代气体的沸点、蒸发焓、临界特征以及输运特性的理论方法，提高筛选替代气体的效率和准确度。
4）深入挖掘替代气体的大气降解寿命与分子结构的关联，寻找降低分子GWP的关键机制，应特别关注除OH自由基降解机理之外的反应过程，建立全方位评价气体环境效应的实验与理论方案。
5）亟需建立能够表征潜在SF6替代气体毒性与可燃性的实验数据库，并以此训练相应的构效关系模型，特别是以量子化学可计算物理量为描述符的模型，结合人工智能、机器学习等新技术，构筑环保绝缘气体的应用安全屏障。
6）测试已知SF6替代气体的灭弧特性，着重探索能够表征气体本征灭弧能力的物理量，建立电弧过程所涉及的化学反应动力学模型，创新评价气体自恢复特性的新理论，同时针对气体及分解产物与电气设备材料的相容性进行理论模拟与仿真，评估原位直接替换SF6的可能性或提出设备改造理论依据。
